In computer science, formal verification is the art and science of proving mathematical theorems that assert the correctness of hardware and software systems. Typically, these theorems are proved using tools like theorem provers, driven by human experts, manipulating assertions according to the rules of mathematical logic. Different kinds of formal verification tools make tradeoffs between generality and automation, and have complementary uses. Formally asserting the correctness of a system involves the formulation of a mathematically precise specification of the system and of its correctness properties of interest (functionality, security, performance, etc.).

From its origins in research and academia, formal verification is now commonplace in hardware development and is finding increasingly wide use in software development as well. This is particularly the case in the blockchain world, where the (often financial) high stakes and the relative immutability (a characteristic shared with hardware) make the need for correctness more pressing than in other software applications. Formal verification provides unparalleled assurance over normal practices like testing and even fuzzing, which cannot check all possible situations but can only sample them.

At Provable, as we take assurance seriously, we have been embracing formal verification, in addition to normal practices like testing and auditing. Our ultimate goal is to apply formal verification to every aspect of the Aleo ecosystem: blockchain, wallets, development tools, applications, etc. Besides formally verifying the consensus algorithm, our focus has been on the development tools, namely the compilation of Leo to R1CS through Aleo instructions.

Leo is Provable’s high-level programming language for zero-knowledge applications. Aleo instructions are Aleo’s intermediate-level assembly language used to represent application code in the Aleo blockchain. R1CS (Rank-1 Constraint System) is a standard low-level representation of circuits used in zero-knowledge proofs. A zero-knowledge proof asserts that a computation has been performed correctly according to its R1CS representation; it does not say whether it has been performed correctly according to its Aleo instructions or Leo representations. This is where formal verification comes into play to complete the picture: by proving theorems asserting that the R1CS representation is equivalent to the Aleo instructions representation, and that the Aleo instructions representation is equivalent to the Leo representation, the zero-knowledge proof effectively extends to the Aleo instructions and Leo code, which are human-readable and human-writable representations.

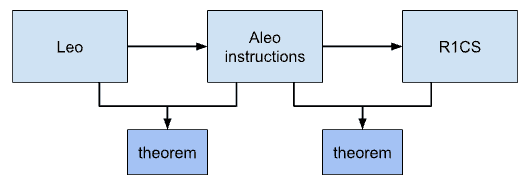
Note that there are two kinds of proofs in play here: zero-knowledge proofs, which provide cryptography-based statistically overwhelming evidence of computational assertions; and formal verification proofs, which provide logic-based unconditional evidence of logical assertions expressed as theorems.

These equivalence theorems among Leo, Aleo instructions, and R1CS rely on a formal specification of the syntax and semantics of Leo and Aleo instructions, as well as of R1CS. These formal specifications have independent value on their own, as they provide mathematically precise and unambiguous definitions of these languages. They also support the development of theorems about these languages (distinct from the equivalence theorems) that validate properties like determinism and other language design criteria.

At the time of this writing, we are working on the formal specifications of Leo and Aleo instructions, and on the generation and checking of theorems for some of the compilation phases in the diagram shown above. As the formal verification tool, we are using ACL2, an industrial-strength general-purpose theorem prover that is popular for both hardware and software verification.

The compilation of Aleo instructions to R1CS builds the zero-knowledge circuits by suitably combining snarkVM gadgets, which are hierarchically organized components. A major focus of our current formal verification work is on the development of theorems that assert the correctness of these gadgets. The theorems mirror the hierarchical structure of the gadgets: theorems for composite gadgets are based on theorems for component gadgets.

We have published and presented our initial work on circuit formal verification at the 2023 Science of Blockchain Conference (SBC) (paper) and at the 2023 ACL2 Workshop (paper). This work is ongoing, and we are interested in collaborating to increase the assurance of Aleo.